來(lái)源：中國(guó)人民教育出版社網(wǎng)，作者：何烈云。

簡(jiǎn)諧運(yùn)動(dòng)在不考慮摩擦和其他阻力等因素的影響時(shí)，振動(dòng)過(guò)程中系統(tǒng)的機(jī)械能守恒，所以不管是單擺還是彈簧振子在振動(dòng)過(guò)程中振幅始終保持不變，這種振動(dòng)稱為無(wú)阻尼振動(dòng)。然而，實(shí)際的振動(dòng)總要受到阻力的影響，由于要克服阻力做功，振動(dòng)系統(tǒng)的機(jī)械能不斷減少。同時(shí)振動(dòng)系統(tǒng)與周圍介質(zhì)相互作用，振動(dòng)向外傳播形成波，隨著波的傳播，系統(tǒng)的機(jī)械能不斷減少，因此振幅也逐漸減小。這種振幅逐漸減小的振動(dòng)叫做阻尼振動(dòng)，阻尼振動(dòng)的圖象如圖1所示。

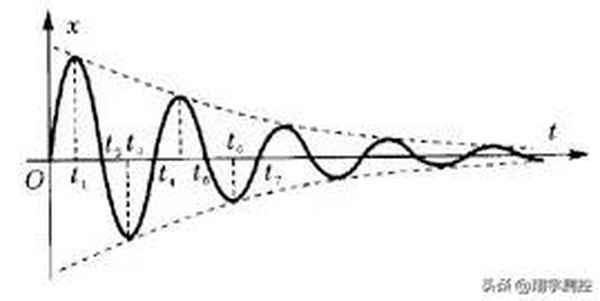
圖1

在這兩方面一般會(huì)存在這樣的疑問(wèn)：

• 一是，阻尼振動(dòng)是否具有“周期性”；
• 二是，阻尼振動(dòng)是否具有“等時(shí)性”（振子連續(xù)兩次通過(guò)平衡位置的時(shí)間間隔相同）。

一、定性分析

要想知道阻尼振動(dòng)是否具有“周期性”，首先要知道什么是機(jī)械振動(dòng)的周期。定義是：物體完成一次全振動(dòng)所需的時(shí)間，叫做振動(dòng)的周期。在周期的定義中存在全振動(dòng)這個(gè)概念，全振動(dòng)是指做機(jī)械振動(dòng)的物體從某個(gè)點(diǎn)出發(fā)，等到下次回到該點(diǎn)時(shí)的運(yùn)動(dòng)狀態(tài)和開(kāi)始振動(dòng)時(shí)的運(yùn)動(dòng)狀態(tài)完全相同，且所用時(shí)間最短。所以能重復(fù)原來(lái)的運(yùn)動(dòng)狀態(tài)（位移、速度、加速度等）的機(jī)械振動(dòng)才是全振動(dòng)，非等幅的阻尼振動(dòng)不是全振動(dòng)，所以它是沒(méi)有周期的。

關(guān)于阻尼振動(dòng)是否具有“等時(shí)性”，有兩種不同的說(shuō)法：

• 第一種說(shuō)法認(rèn)為具有“等時(shí)性”，理由是阻尼振動(dòng)的振幅雖然在不斷減小，但可以看成是由很多個(gè)振幅不斷減小的簡(jiǎn)諧運(yùn)動(dòng)的疊加，由于簡(jiǎn)諧運(yùn)動(dòng)具有等時(shí)性，它的周期與振幅無(wú)關(guān)，所以阻尼振動(dòng)和簡(jiǎn)諧運(yùn)動(dòng)的相位是一致的，節(jié)奏也是相同的，所以具有“等時(shí)性”。
• 第二種說(shuō)法認(rèn)為不具有“等時(shí)性”，理由是物體做阻尼振動(dòng)時(shí)，由于機(jī)械能的損失。振子前后兩次通過(guò)同一點(diǎn)時(shí)，后一次的速度肯定比前一次的小。這樣，從平衡位置到達(dá)最大位移處的平均速度總比返回時(shí)的平均速度大，所以回來(lái)就變慢了，對(duì)應(yīng)的時(shí)間也就長(zhǎng)了。按這種推理，阻尼振動(dòng)的振動(dòng)節(jié)奏會(huì)變得越來(lái)越慢，最后停止下來(lái)，周期變?yōu)闊o(wú)窮大，所以不具有“等時(shí)性”。

二、定量分析

彈簧振子在油中或較粘稠的液體中的緩慢運(yùn)動(dòng)是阻尼振動(dòng)的典型例子，如圖2所示，由流體力學(xué)可知，彈簧振子在油中或較粘稠的液體中運(yùn)動(dòng)時(shí)所受阻力的大小和速度的大小成正比，由牛頓第二定律，得

圖2

式中，Υ 是阻尼系數(shù)。兩邊除以m，得

令

ω0為振動(dòng)系統(tǒng)的固有圓頻率；β 為阻尼系數(shù)，和振動(dòng)系統(tǒng)的性質(zhì)以及介質(zhì)的性質(zhì)有關(guān)。于是，方程可寫為

這里我們討論的是阻力很小的欠阻尼狀態(tài)的阻尼振動(dòng)，即β＜ω0，由上式可求出彈簧振子中質(zhì)點(diǎn)的運(yùn)動(dòng)學(xué)方程為

式中，A 和a 為待定常數(shù)，由初始條件決定。此式中包含兩個(gè)因子，Ae-βt 表示隨時(shí)間衰減的振幅，cos(ω't＋a) 表示振動(dòng)以ω' 為圓頻率周期地變化，二因子相乘表示質(zhì)點(diǎn)做運(yùn)動(dòng)范圍不斷縮小的往復(fù)運(yùn)動(dòng)。由于質(zhì)點(diǎn)的運(yùn)動(dòng)狀態(tài)不可能每經(jīng)過(guò)一定時(shí)間便完全重復(fù)出現(xiàn)，因此阻尼振動(dòng)不是周期運(yùn)動(dòng)。不過(guò)，cos(ω't＋a) 是周期變化的，它保證了質(zhì)點(diǎn)每連續(xù)兩次通過(guò)平衡位置并沿相同方向運(yùn)動(dòng)的時(shí)間間隔是相同的，可見(jiàn)“等時(shí)性”具有非常嚴(yán)格的條件。而且由于

大于彈簧振子系統(tǒng)的固有周期T=2π/ω0，可見(jiàn)阻尼振動(dòng)的節(jié)奏變慢了。

三、結(jié) 論

比較由定性分析和定量分析得出的結(jié)論，阻尼振動(dòng)不具有“周期性”的觀點(diǎn)是相同的，但關(guān)于阻尼振動(dòng)是否具有“等時(shí)性”的分析結(jié)果是不一樣的。

只有通過(guò)定量分析的結(jié)論才是可靠的、正確的，仔細(xì)分析定性分析的兩種說(shuō)法中，推理都不嚴(yán)密并且是片面的，從而導(dǎo)致錯(cuò)誤的結(jié)論。

• 定性分析中的第一種說(shuō)法沒(méi)有考慮到振子做阻尼振動(dòng)時(shí)，由于阻力的影響回復(fù)力的大小不再和位移成正比，得出“阻尼振動(dòng)和簡(jiǎn)諧運(yùn)動(dòng)相位是一致的，節(jié)奏也是相同的”的錯(cuò)誤結(jié)論。
• 定性分析中的第二種說(shuō)法只考慮了振子從平位置出發(fā)到達(dá)最大位移處，又從最大位移處返回到平衡位置，即在圖1中的0～2 或2～4 這段時(shí)間的運(yùn)動(dòng)情況，沒(méi)有把運(yùn)動(dòng)過(guò)程進(jìn)行整體分析，從而忽視了在平均速度減小的同時(shí)，振子從平衡位置出發(fā)往復(fù)一次所經(jīng)過(guò)的路程也變短了，導(dǎo)致得出錯(cuò)誤的結(jié)論。

綜上所述，阻尼振動(dòng)不是周期性運(yùn)動(dòng)，但是質(zhì)點(diǎn)連續(xù)兩次通過(guò)平衡位置并沿相同方向運(yùn)動(dòng)所需的時(shí)間間隔是相同的。討論阻尼振動(dòng)時(shí)不能照搬簡(jiǎn)諧運(yùn)動(dòng)的規(guī)律，也不能做簡(jiǎn)單的定性分析，必要時(shí)還要做定量分析，否則就容易得出錯(cuò)誤的結(jié)論。

參考文獻(xiàn)：

漆安慎，杜彈英。力學(xué)。北京：高等教育出版社，1997．280～281

北京神州翔宇技術(shù)有限公司